2022年成考高起点每日一练《数学(文史)》6月20日专为备考2022年数学(文史)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、某学校为新生开设了4门选修课程,规定每位新生至少要选其中3门,则一位新生不同的选课方案共有 ( )
- A:7种
- B:4种
- C:5种
- D:6种
答 案:C
2、不等式|x-2|<1的解集是()
- A:{x|-1<x<3}
- B:{x|-2<x<l}
- C:{x|-3<x<1}
- D:{x|1<x<3}
答 案:D
解 析:|x-2|<1=>-1<x-2<1=>1<x<3,故不等式的解集为{x|1<1<3}.
3、过点(0,1)且与直线x+y+1=0垂直的直线方程为( )
- A:y=x+1
- B:y=2x+1
- C:y=x
- D:y=x-1
答 案:A
解 析:与直线x+y+1=0垂直的斜率是1,并且该直线同时过点(0,1),所以该直线的方程应该为y-1=1*(x-0),即y=x+1,答案为:A
4、设集合P={x|-1≤x≤3},N={x|2≤x≤4},则P∪N是()。
- A:{x|2≤x≤3}
- B:{x|2<x<3}
- C:{x|-1<x<4}
- D:{x|-1≤x≤4}
答 案:D
解 析:由已知条件P={x|-1≤x≤3},N={x|2≤x≤4},∴P∪N={x|-1≤x≤4}。
主观题
1、已知A,B为⊙O上的两点,且AB= ∠ABO=30°.求⊙O的半径。
∠ABO=30°.求⊙O的半径。
答 案:设⊙O的半径为r,则OA=OB=r。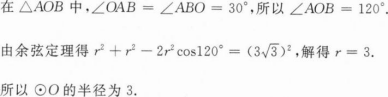
2、(I)求{an}的通项公式;
答 案:a2??=1/2+d??,??a5??=1/2+4d 由已知得(1/2+d)2=1/2(1/2+4d) 解得d=0(舍去),d或=1. 所以{an}的通项公式为 an=1/2+(n-1)×1=n-1/2 ????
3、(I)求E的离心率;
答 案:由题设知△AF1F2为直角三角形,且 设焦距|F1F2|= 2c,则|AF2|=3/2c如,|AF1|=5/2c,2a=|AF1|+|AF2|= 4c.
所以离心率
设焦距|F1F2|= 2c,则|AF2|=3/2c如,|AF1|=5/2c,2a=|AF1|+|AF2|= 4c.
所以离心率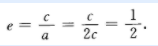
4、
答 案:(I)由


填空题
1、若平面向量a=(x,1),b=(1,-2),且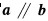 ,则x=
,则x=
答 案:-1/2
2、等比数列{an}中,若a2=8,公比为1/4,则a5=
答 案:1/8
解 析:【考情点拨】本题主要考查的知识点为等比数列.【应试指导】
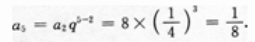
精彩评论