2023年成考高起点每日一练《数学(理)》8月15日专为备考2023年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、 展开式中,末3项的系数(a,x 均未知) 之和为()
展开式中,末3项的系数(a,x 均未知) 之和为()
- A:22
- B:12
- C:10
- D:-10
答 案:C
解 析: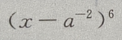

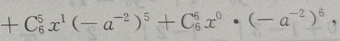 末三项数之和为
末三项数之和为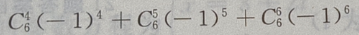
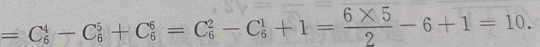
2、给出下列两个命题:①如果一条直线与一个平面垂直,则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点,在二面角的两个面内分别作射线,则这两条射线所成的角为该二面角的平面角.则()
- A:①②都为真命题
- B:①为真命题,②为假命题
- C:①为假命题,②为真命题
- D:①②都为假命题
答 案:B
解 析:一条直线与平面垂直,则直线与平面内的任意一条直线垂直,故①为真命题;二面角的两条射线必须垂直于二面角的棱,故②为假命题,因此选B选项.
3、已知复数z=a+bi,其中a, 且b≠0,则()
且b≠0,则()
- A:

- B:
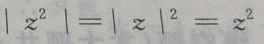
- C:

- D:

答 案:C
解 析:注意区分

4、设集合A={0,1},B={0,1,2},则A∩B=()
- A:{1,2}
- B:{0,2}
- C:{0,1}
- D:{0,1,2}
答 案:C
解 析: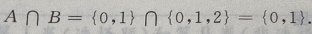
主观题
1、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
答 案:(Ⅰ)由题意知(如图所示) 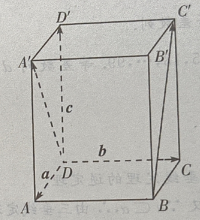
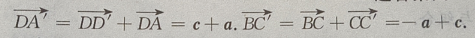
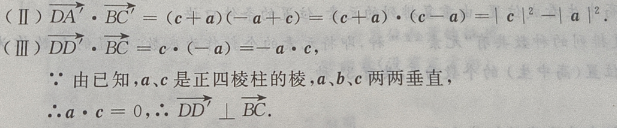
2、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程;
(II)求f(x)的极值.
答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
3、已知等差数列前n项和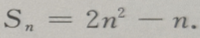 (Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
(Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
答 案: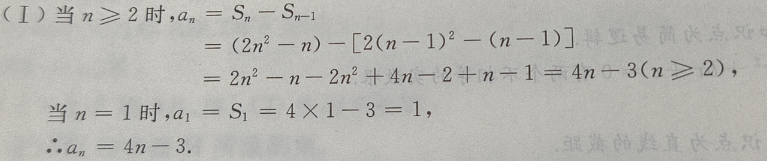

4、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c.
答 案:由已知得 解得
解得
填空题
1、函数 的定义域是()
的定义域是()
答 案: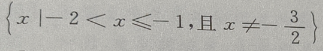
解 析: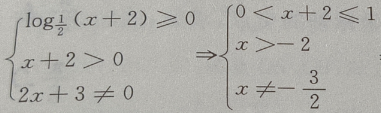
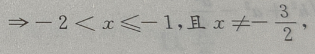 所以函数
所以函数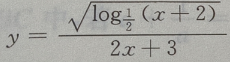 的定义域是
的定义域是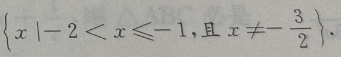
2、若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
答 案: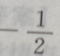
解 析:由于a//b,故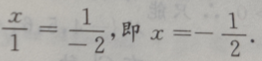
精彩评论