2023年成考高起点每日一练《数学(理)》8月12日专为备考2023年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
单选题
1、5名高中毕业生报考3所院校,每人只能报一所院校,则有()种不同的报名方法
- A:
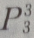
- B:
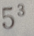
- C:
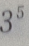
- D:

答 案:C
解 析:将院校看成元素,高中生看成位置,由重复排列的元素、位置的条件口诀: “元素可挑剩,位置不可缺”,重复排列的种数共有 种,即将元素的个数作为底数,位置的个数作为指数.即:元素(院校)的个数为 3,位置(高中生)的个数为5,共有
种,即将元素的个数作为底数,位置的个数作为指数.即:元素(院校)的个数为 3,位置(高中生)的个数为5,共有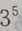 种。
种。
2、将一颗骰子抛掷1次,到的点数为偶数的概率为
- A:

- B:
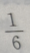
- C:

- D:
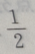
答 案:D
解 析:一颗骰子的点数分别为1,2,3,4,5,6,其中偶数与奇数各占一半,故抛掷1次,得到的点数为偶数的概率为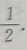
3、已知偶函数y=f(x),在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0 4、在△ABC中,已知2B= A+C, 答 案:A 解 析:在△ABC中,A+B+C=π,A+C=π-B,① 因为2B=A+C,②
由①②得2B=π-B, 主观题 1、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 答 案:如图, 2、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c. 答 案:由已知得 3、已知直线l的斜率为1,l过抛物线C: 答 案:(I)C的焦点为 4、在△ABC中,B=120°,BC=4,△ABC的面积为 答 案:由△ABC的面积为 填空题 1、lg(tan43°tan45°tan47°)=()
答 案:0 解 析:lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0 2、若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
答 案: 解 析:由于a//b,故 = ac,则B-A=()
= ac,则B-A=()
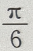
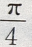
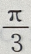

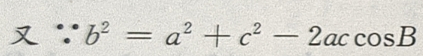
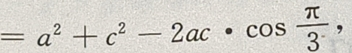
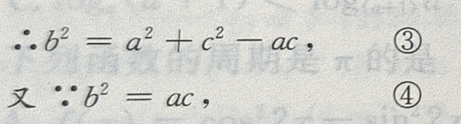 由③④得
由③④得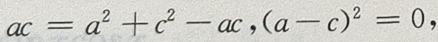 a=c。所以A=C,又
a=c。所以A=C,又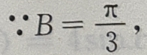 所以△ABC为等边三角形,则B-A=0
所以△ABC为等边三角形,则B-A=0
 AB=120m,求河的宽
AB=120m,求河的宽

 ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
 解得
解得
 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
 ,求AC.
,求AC. 得
得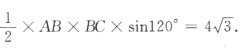 所以AB =4.因此
所以AB =4.因此 所以
所以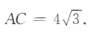
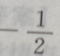
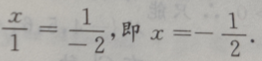
精彩评论