2023年成考专升本每日一练《高等数学二》10月4日专为备考2023年高等数学二考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、在x趋向于()时, 为无穷小量.
为无穷小量.
- A:2
- B:1
- C:-1
- D:+∞
答 案:D
解 析:A项,当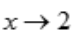 时,
时,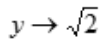 ;B项,当
;B项,当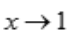 时,
时,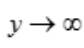 ;C项,由题意x≥0,且x≠1,故x不能趋向于-1;D项,当
;C项,由题意x≥0,且x≠1,故x不能趋向于-1;D项,当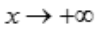 时,因为分子x的次幂小于分母中x的次幂,故
时,因为分子x的次幂小于分母中x的次幂,故 ,即为无穷小.
,即为无穷小.
2、设函数z=sin(xy),则下列结论正确的是().
- A:
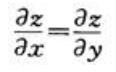
- B:
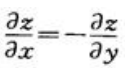
- C:
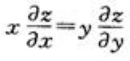
- D:
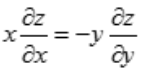
答 案:C
解 析: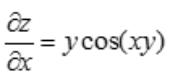 ,
,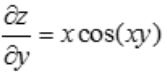 ,所以
,所以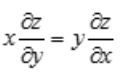 .
.
主观题
1、设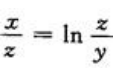 ,求
,求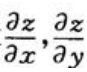 .
.
答 案:解:将方程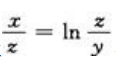 写成
写成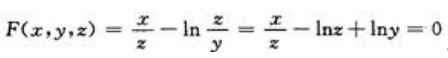 .因为
.因为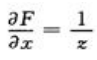 ,
,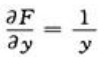 ,
,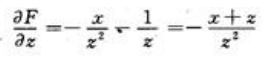 ,所以
,所以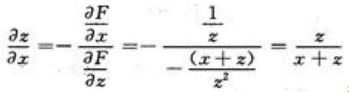 ,
,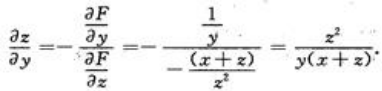
2、盒中装着标有数字1、2、3、4的乒乓球各2个,从盒中任意取出3个球,求下列事件的概率:(1)A={取出的3个球上最大的数字是4}.
(2)B={取出的3个球上的数字互不相同}.
答 案:解:基本事件任意取出3个球共有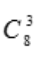 种.(1)取出的3个球上最大的数字是4,有两种可能,即从中取出一个数字为4的球或取出两个数字为4的球,取出一个数字为4的球有
种.(1)取出的3个球上最大的数字是4,有两种可能,即从中取出一个数字为4的球或取出两个数字为4的球,取出一个数字为4的球有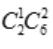 种,取出两个数字为4的球有
种,取出两个数字为4的球有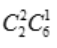 种.事件A中的基本事件为
种.事件A中的基本事件为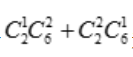 种.所以
种.所以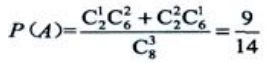 (2)事件B中的基本事件数的计算可以分两步进行:
(2)事件B中的基本事件数的计算可以分两步进行:
先从1,2,3,4的4个数中取出3个数的方法为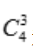 种.
种.
由于每1个数有2个球,再从取出的3个不同数字的球中各取1个球,共有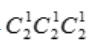 种.
种.
根据乘法原理可知取出的3个球上的数字互不相同的取法共有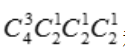 种.
种.
所以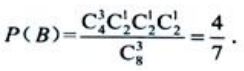
填空题
1、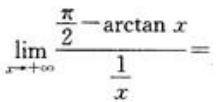 ().
().
答 案:1
解 析: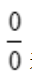 型,由洛必达法则得
型,由洛必达法则得 .
.
2、当x→0时,f(x)与sin2x是等价无穷小量,则 ().
().
答 案:1
解 析:根据等价无穷小定义,可知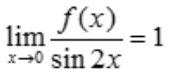 .
.
简答题
1、求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积.
答 案:如图所示,在x=a出切线的斜率为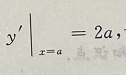 切线方程为
切线方程为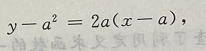

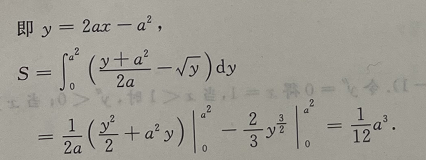
2、计算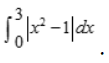
答 案: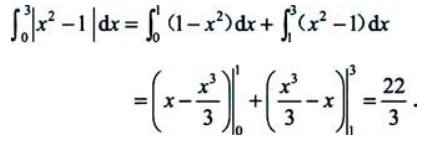
精彩评论