2023年高职单招每日一练《数学》10月1日专为备考2023年数学考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
判断题
1、任一事件A,其概率为P(A),则有0≤P(A)≤1.()
答 案:对
解 析:随机事件的概率大于0小于1;必然事件的概率等于1,不可能事件的概率等于0。所以任意事件的概率都要满足0≤P(A)≤1。
2、二项式(x+1)5的展开式共6项。()
答 案:对
解 析:n次方的展开式有n+1项,5次方的展开式有6项
单选题
1、两百多年以前,在清代乾隆五十年的时候,乾隆皇帝在乾清宫摆下千叟宴,3900多位老年人应邀参加宴会。其中有一位客人的年纪特别大。乾隆帝说了,不过不是明说,而且是出了一道对联的上联:花甲重开,外加三七岁月。大臣纪晓岚在一旁凑热闹,也说一说这位老寿星的岁数,当然也不是明说,而是对出了下联:古稀双庆,又多一个春秋。这位年龄特大的老寿星岁数是()岁。
- A:140
- B:141
- C:101
- D:130
答 案:B
解 析:先看上联。花甲就是甲子,一个甲子是60年时间。“花甲重开”,是说经过了两个甲子,就是120年,这还不够,还要“外加三七岁月”,3和7相乘,是21年,所以总数是60×2十3×7-141(岁)。再看下联。“古稀”是70岁。“古稀双庆”,是说这位老先生居然两次庆贺古稀,度过了两个70年,并且不止这些,还“又多一个春秋”,总数是70×2+1-141(岁)。故选B
2、若|a|=-a,则a一定是()
- A:负数
- B:正数
- C:非负数
- D:非正数
答 案:D
解 析:根据绝对值的定义,绝对值等于它的相反数的数是负数或零。∵a的相反数是-a,且|a|=-a,∴a一定是负数或零
多选题
1、下列关于圆的叙述正确的有()
- A:对角互补的四边形是圆内接四边形
- B:圆的切线垂直于圆的半径
- C:正多边形中心角的度数等于这个正多边形一个外角的度数
- D:过圆外一点所画的圆的两条切线长相等
答 案:ACD
解 析:A、由圆内接四边形定义得:对角互补的四边形是圆内接四边形,A选项正确;B、圆的切线垂直于过切点的半径,B选项错误;C、正多边形中心角的度数等于这个正多边形一个外角的度数,都等于360°/n,C选项正确;D、过圆外一点引的圆的两条切线,则切线长相等,D选项正确。故选:ACD
2、已知函数y=1/2sin2x则()
- A:函数最大值为2
- B:函数最大值为1/2
- C:周期
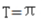
- D:周期
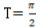
答 案:BC
解 析:A:sin2x最大值为1,则y=1/2sin2x的最大值为1/2,故A错B对。C:T=2π/W=2π/2=π,故C对D错
主观题
1、已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域;
(2)若f(x)<1,求x的取值范围.
答 案:(1)根据题意可得,3x-1>0,解得 所以函数f(x)的定义域是
所以函数f(x)的定义域是 (2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
(2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
 所以x的取值范围是
所以x的取值范围是
2、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
填空题
1、已知作用在坐标原点的三个力f1=(1,2),f2=(2,4),f3=(-3,6),则它们的合力f的坐标是________.
答 案:(0,12)
2、设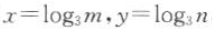 ,其中m,n是正实数,则mn=().
,其中m,n是正实数,则mn=().
答 案:3x+y
解 析:由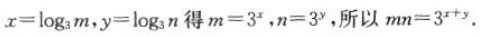
精彩评论